题目描述：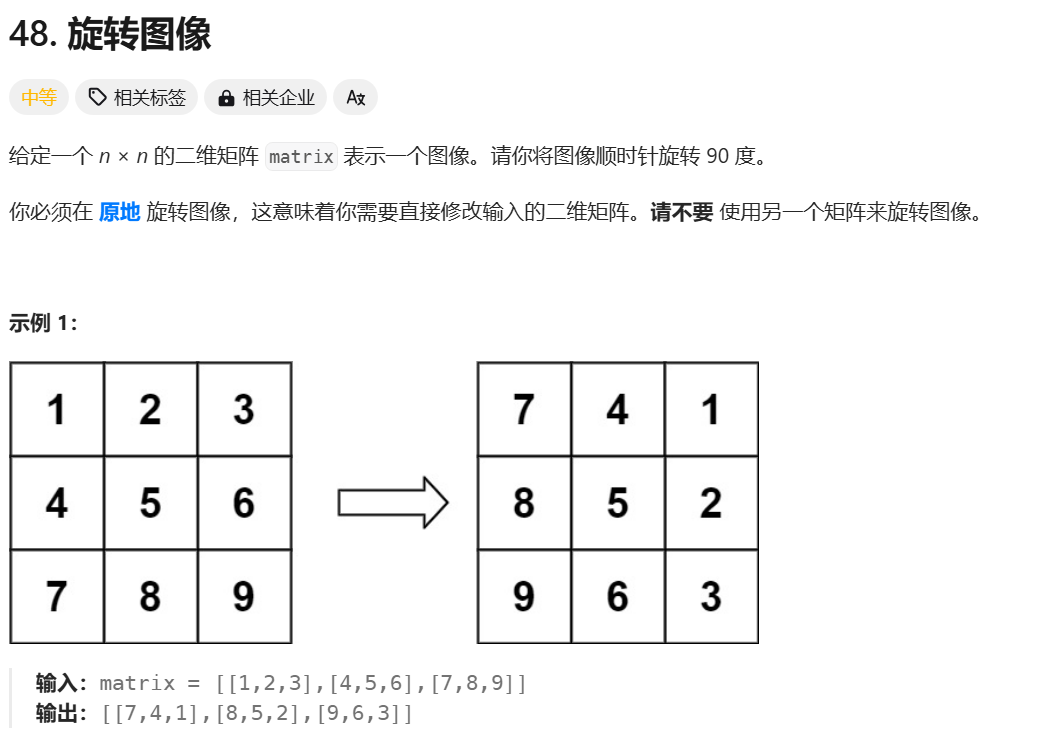

方法1：用一个辅助矩阵来存旋转后的矩阵，然后把辅助矩阵赋值给原矩阵（矩阵第一列是旋转过的第一行，第二列是第二行）

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        vector<vector<int>> result;
        for(int i=0;i<n;i++){
            vector<int> temp;
            for(int j=n-1;j>-1;j--){
                temp.push_back(matrix[j][i]);
            }
            result.push_back(temp);
        }
        matrix = result;
    }
};

方法2：原地旋转，对于一个矩阵，有以下几种旋转

上下对称：matrix[i][j] -> matrix[n-i-1][j]，（列不变）
左右对称：matrix[i][j] -> matrix[i][n-j-1]，（行不变）
主对角线对称：matrix[i][j] -> matrix[j][i]，（行列互换）
副对角线对称：matrix[i][j] -> matrix[n-j-1][n-i-1] （行列均变，且互换）

对于该题

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for(int i=0;i<n/2;i++){
            for(int j=0;j<n;j++){
                swap(matrix[i][j],matrix[n-1-i][j]);
            }
        }

        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                swap(matrix[i][j],matrix[j][i]);
            }
        }
    }
};

注：主对角线对称时，一定是 j=i！