1、激活函数
为什么需要激活函数:深度学习模型本质上是对函数的拟合,但是神经网络层都是线性,无法进行非线性建模,所以需要引入非线性的激活函数
特点:非线性、可微性(不然无法反向传播)、单调性)
为什么通常需要单调性:1、若不单调,反向传播更新时,导数有正有负,梯度方向不稳定;2、可能出现多个极小值,增加训练难度,难以收敛到全局最优解
分类:有饱和激活函数与非饱和激活函数,sigmoid 与 Tanh都是饱和的,即输入较大或较小时,输出变化不敏感,导致梯度过小,即梯度消失(所以饱和激活函数对于权重矩阵的初始化特别留意,初始化权重过大,可能很多神经元得到一个比较小的梯度,致使神经元不能很好的更新权重提前饱和,神经网络就几乎不学习)
sigmoid激活函数:
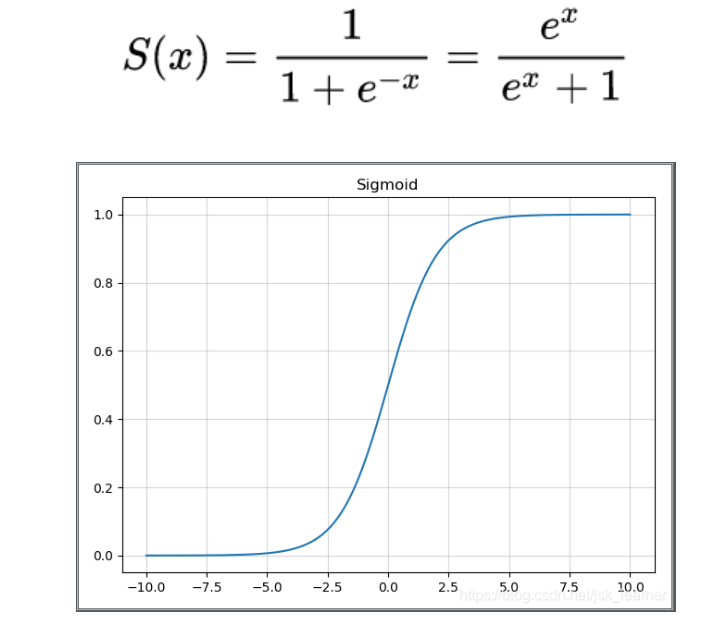
其导数如下图:
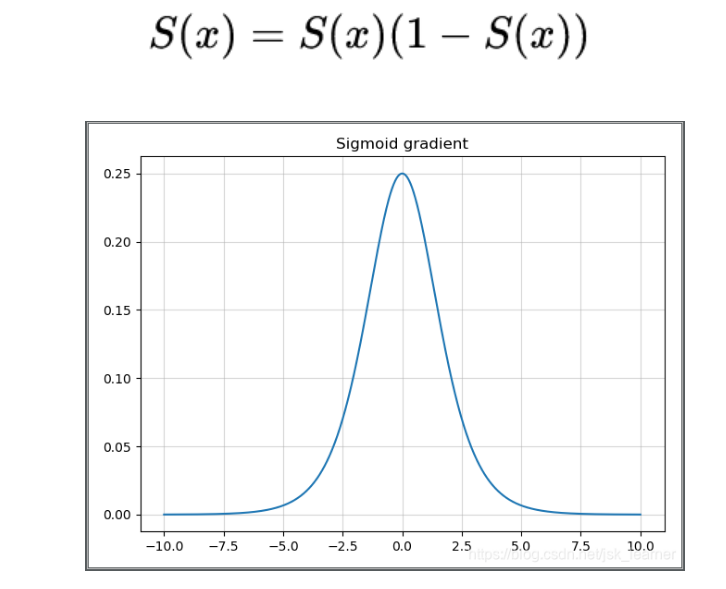
特点:
输出映射到 0-1
导数为 0-0.25,神经网络中有多个激活函数,如果多个 0-0.25 的值相乘,可能出现梯度消失(梯度弥散)问题
函数输出的期望不是0,梯度有向特点方向移动的趋势,降低更新效率
sigmoid 存在幂运算,计算复杂度大
是饱和激活函数
Tanh激活函数:

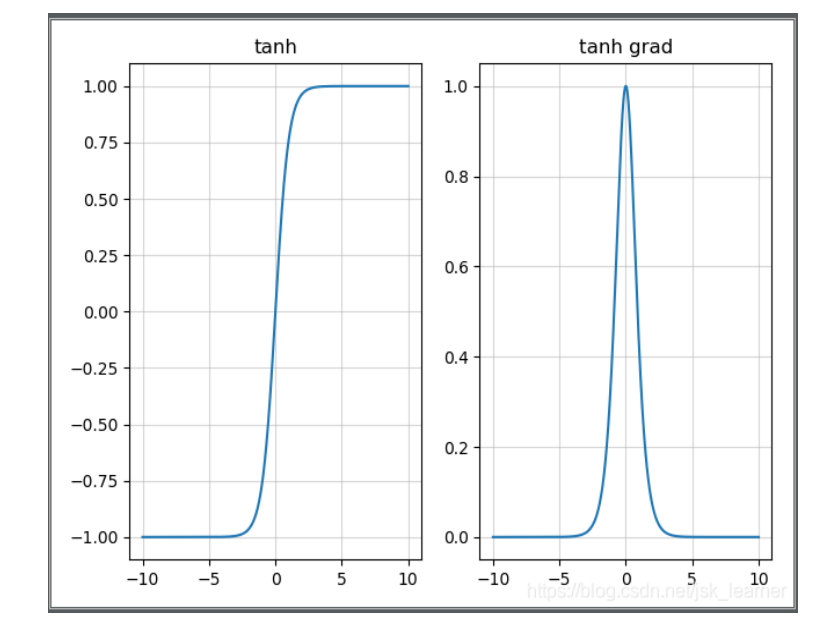
特点:
输出映射到 -1-1
导数为 0-1
梯度消失问题存在一点点改善
任然存在计算复杂度、梯度消失的问题
是饱和激活函数
ReLU激活函数
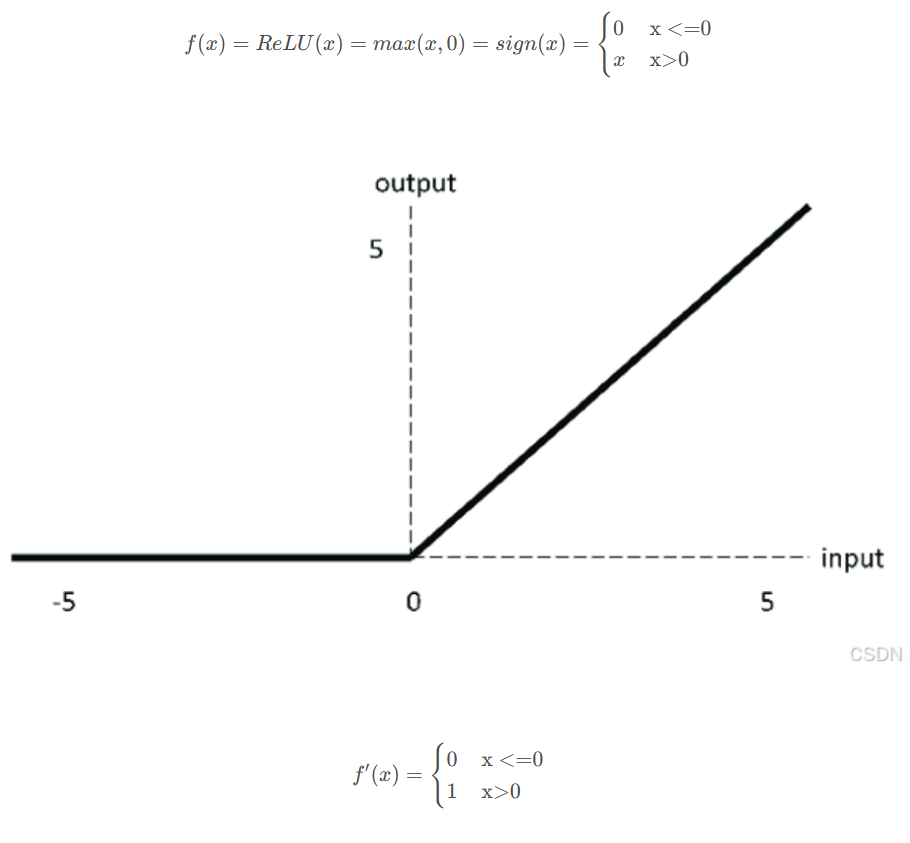
特点:
是非饱和激活函数,避免了梯度消失的问题
计算复杂度低
训练神经网络的时候,一旦学习率没有设置好,第一次更新权重的时候,输入是负值,那么这个含有ReLU的神经节点就会死亡,再也不会被激活,所以,要设置一个合适的较小的学习率,来降低这种情况的发生
Softmax激活函数
是一种归一化函数,其将输入值映射为0-1之间的概率实数,常用于多分类
2、反向传播

3、梯度消失(梯度弥散)和梯度爆炸
梯度消失:softmax等激活函数,在值较大或较小时,变化很小,导致梯度很小,反向传播不断相乘导致梯度消失的问题
梯度爆炸:神经网络有多次连乘,不断相乘梯度可能越来越大,出现梯度爆炸的问题
4、归一化的方法
最大最小值归一化

缺点:对异常值敏感,最大最小值容易被异常值影响
Z-score标准化

对数据鲁棒性比较强,但是可能输出负数
归一化和标准化区别:归一化是将数据缩放到一个固定的区间,不改变数据的分布,受异常点影响大
标准化是调整数据的分布,比如说变成均值为0,标准差为1的分布,更鲁棒,受异常点影响更小
如果对输出结果有特定的要求,数据较为稳定,不存在极端的极大极小值,用归一化
如果数据存在较多异常值或者噪声,用标准化
5、去除异常点的方法
Z-score的方法,把每个数据标准化后的值和一个阈值对比,大于阈值上界或者小于阈值下界的就剔除
通过聚类的方法去剔除异常点
用散点图或者热力图的方式来剔除异常点
6、损失函数
回归损失函数:
MSE(均方误差)- 预测值和真实值距离的平方,MAE(平均绝对误差)- 预测值和真实值误差的绝对值

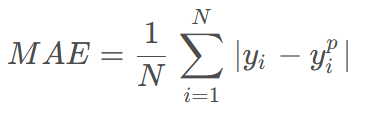
MSE因为有平方,所以对异常值很敏感,鲁棒性低于MAE
MAE因为导数不连续(需使用次梯度优化),求解效率更低,收敛更慢
次梯度优化:处理非光滑凸函数的核心方法,是一个集合,可能包含多个方向的梯度
分类损失函数
交叉熵损失函数,描述了两个概率分布之间的距离(log里面是标签),KL散度(两个概率相等时,KL散度为0)
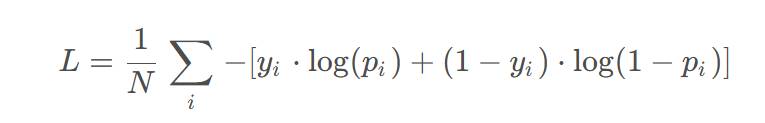
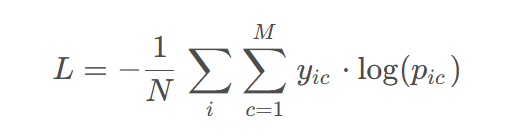
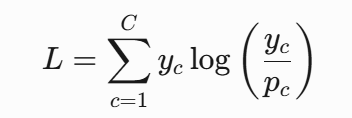
交叉熵 = KL散度 + 真实分布的熵,如果是one-hot编码,交叉熵等于KL散度,one-hot编码真实分布的熵为0
熵:用来描述一个概率分布,也就是一个信息的不确定性、混乱程度,熵越大,也就表示这个概率分布越混乱,不确定性越高
交叉熵和熵前面都有个负号,KL散度没有
分类为什么用交叉熵不用mse
因为分类通常会有sigmoid这样的激活函数在里面,sigmoid激活函数是饱和的,在x大于5的时候,梯度是很小的,mse反向传播的时候,计算导数的时候,会有一项sigmoid的导数,可能导致,误差大的时候,反而训练慢,但是交叉熵的话,求导数过程中,可以巧妙的把sigmoid的导数消去,所以不用mse
7、优化器的介绍
梯度下降
梯度下降:用所有样本,效率低
随机梯度下降:用小批量的样本
缺点:学习率固定,震荡大,收敛比较慢
所以引入动量梯度下降,在计算梯度的时候,引入一个动量项,用来累计梯度变化方向,减少震荡,加快收敛
而普通的梯度下降,可能会使迭代点超出可行域,投影梯度下降则在每次参数更新后,将更新的参数投影到可行域上,确保迭代点始终在可行域内

Adam和AdanW
Adam结合了动量和自适应学习率,通过计算梯度的一阶矩(均值)和二阶矩(方差),融入到梯度下降公式中,同时在计算梯度的时候,涉及了L2正则化,防止了模型的过拟合(梯度是根据损失函数计算,损失函数中有正则化)
缺点:Adam会自适应调整缩放更新量,这就导致,L2正则化项也被缩放,出现正则化不均的问题,影响模型效果
引入了AdamW,采样了一种去耦合的方式,将原本梯度计算中的L2正则化项,移到了参数更新的公式中去,避免了正则化不均的问题

8、L1正则化和L2正则化的分析
都是为了降低过拟合的问题
L1正则化:在损失函数中添加权重的绝对值之和
L2正则化:在损失函数在添加权重的平方和
L1正则化对异常值更鲁棒,L2正则化对异常值更敏感(平方会放大异常值的影响)
L1正则化可能产生稀疏解(部分权重被压缩为0),L2正则化则倾向于让权重接近0但不为0
为什么可能产生稀疏解:因为 L1 正则化的导数是不连续的,在零点附近有正有负,可能会导致权重在零点附近震荡,被压缩为0
9、介绍下神经网络中的误差、偏差、方差
误差:误差表示模型预测结果与真实值的差异,模型的目标就是通过训练减少这种误差
偏差:偏差表示模型预测的平均误差,一个模型如果是高偏差的,也就是发生了欠拟合
方差:方差表示模型预测值的变化程度,反映了模型对噪声的敏感程度,一个模型如果是高方差的,即对随机噪声过于敏感,模型过于复杂,也就是发生了过拟合
10、介绍下模型的欠拟合、过拟合
从数学角度来看,欠拟合是模型一个高偏差的拟合结果,过拟合是模型的一个高方差的拟合结果
从表现来看的话,欠拟合是指模型在训练集和测试集上变现均不佳,过拟合是值模型在训练集上表现很好,在测试集上表现不佳(泛化性不强)
过拟合解决:正则化、Dropout、降低模型复杂度、通过旋转、加噪声的方式进行数据增强、引入集成学习降低方差
欠拟合解决:减少正则化、增强模型复杂度、通过特征工程添加新特征或者组合特征
11、样本不均衡的处理方法
12、参数初始化的方法
零初始化:可能会带来梯度消失,一般仅适用于偏执初始化;同时,零初始化可能会带来对称更新的问题,神经元会因为输入相同、权重相同,计算出完全相同的梯度;并且抑制了模型的多样性,即抑制了模型的学习能力
随机初始化:高斯(正态)分布,均匀分布,如果方差较大或者较小,可能发生梯度爆炸或者梯度消失
Xavier初始化,Xavier初始化将权重初始化为均匀分布或高斯分布,其方差取决于前一层神经元数量n和后一层神经元数量m,搭配 Sigmoid 或 Tanh 等饱和激活函数,保证前向传播的方差稳定
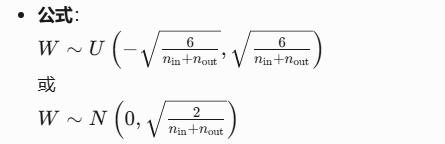
He初始化,根据每一层的激活函数的特性来设置权重的初始范围,缓解ReLU在初始化时的“神经元死亡”问题(避免大量值集中在负区间)


