题目描述：

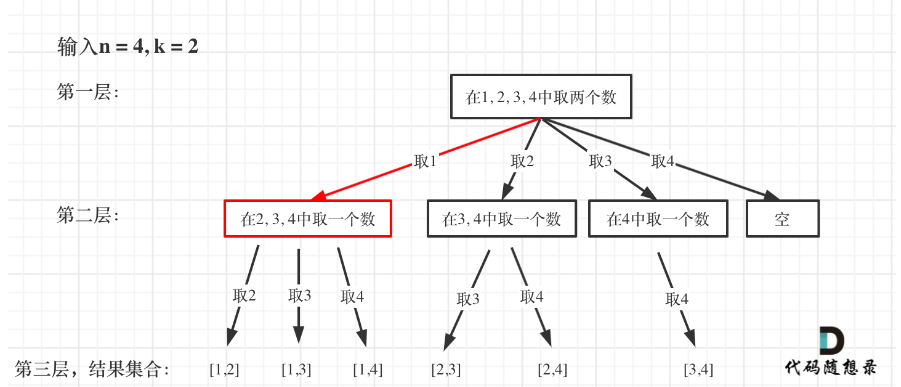
方法1：回溯，startIndex来记录下一层递归，搜索的起始位置

class Solution {
public:
    void backtrack(int n,int k,int StartIndex,vector<vector<int>>&result,vector<int>data){
        if(data.size()==k){
            result.push_back(data);
            return;
        }
        for(int i=StartIndex;i<=n;i++){
            data.push_back(i);
            backtrack(n,k,i+1,result,data);
            data.pop_back();
        }
    }

    vector<vector<int>> combine(int n, int k) {
        vector<int>data;
        vector<vector<int>>result;
        backtrack(n,k,1,result,data);
        return result;
    }
};

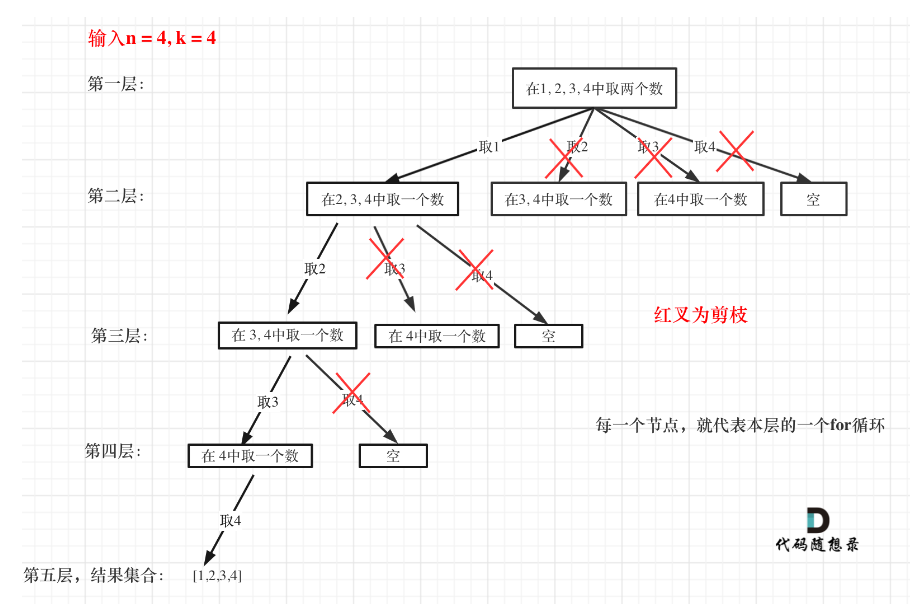
优化，引入剪枝操作，i<=n会所有枝干都遍历，但是实际上是不需要的

比如n = 4，k = 4的话，第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了

剪纸操作，其实就是对for循环条件进行验证

data.size()：已经选择的个数

k-data.size()：还需选择的个数

n-(k-data.size())+1：最少要从哪开始遍历才满足

class Solution {
public:
    void backtrack(int n,int k,int StartIndex,vector<vector<int>>&result,vector<int>data){
        if(data.size()==k){
            result.push_back(data);
            return;
        }
        for(int i=StartIndex;i<=n-(k-data.size())+1;i++){
            data.push_back(i);
            backtrack(n,k,i+1,result,data);
            data.pop_back();
        }
    }

    vector<vector<int>> combine(int n, int k) {
        vector<int>data;
        vector<vector<int>>result;
        backtrack(n,k,1,result,data);
        return result;
    }
};