题目描述：

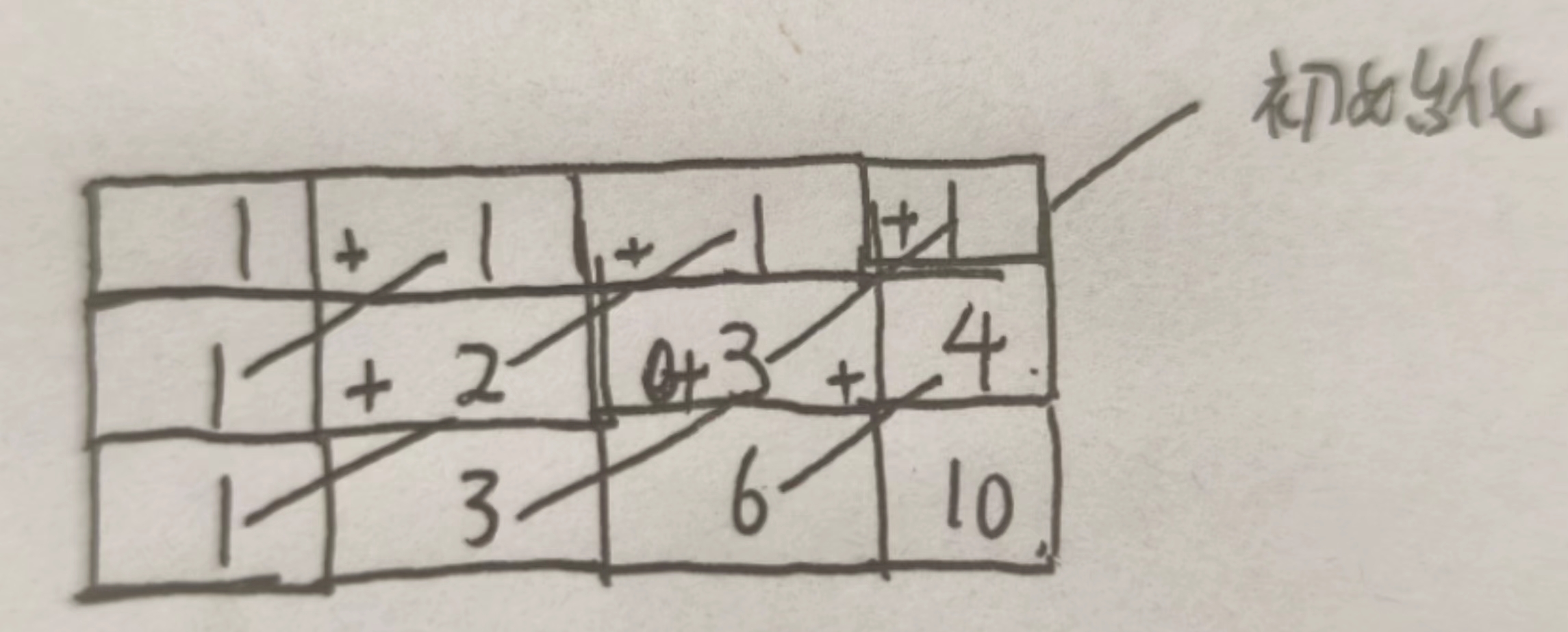
方法1：动态规划，dp[i][j]表示到第 i-1 行第 j-1 列不同路径，dp[i][j] = dp[i-1][j] + dp[i][j-1];其中第一列和第一行固定只有一种路径，从第二行第二列开始遍历，保证可以填满dp数组

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m,vector<int>(n,0));
        for(int i=0;i<n;i++) dp[0][i] = 1;//第一行只有一条路径
        for(int i=0;i<m;i++) dp[i][0] = 1;//第一列只有一条路径
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

方法2：优化空间复杂度， d(i,j)仅与第 i 行和第 i−1 行的状态有关，因此可以使用滚动数组代替代码中的二维数组，使空间复杂度降低为 O(n)

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int>dp(n,1);
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++) dp[j] += dp[j-1] ;
        }
        return dp[n-1];
    }
};