题目描述：

方法1：回溯算法

方法2：动态规划

sum是固定的，target也是固定的，有式子left + right = sum，left - right = target，设left为背包容量，装满left背包的策略总数即为题解，left = (target + sum) / 2

初始dp[i][j]：使用下标为[0, i]的nums[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种方法

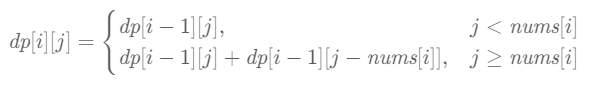
比如示例1，left为4，做题时多加一行，不然要分情况讨论，见第三个代码块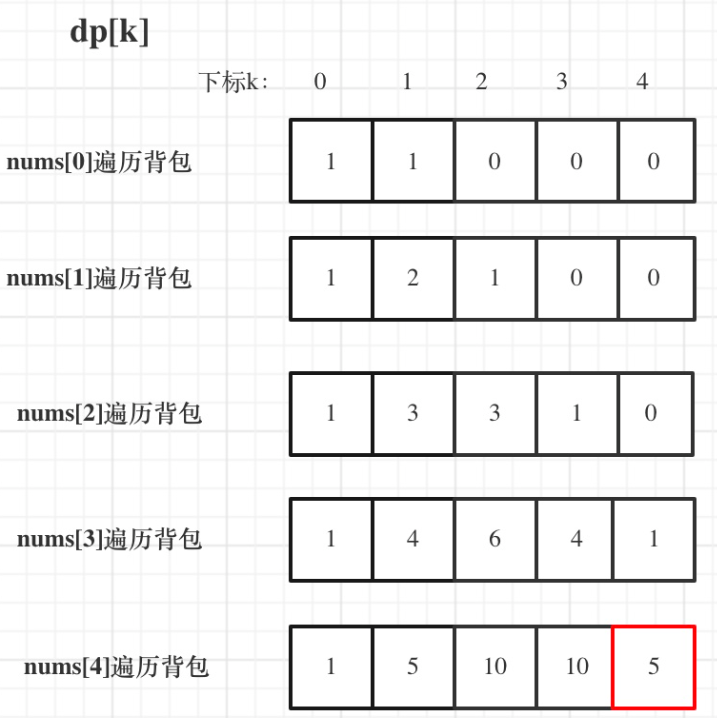

二维

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int i=0;i<nums.size();i++) sum += nums[i];
        if (sum < abs(target) || (sum + target) % 2 != 0) return 0;//left一定要是偶数

        int left = (sum + target)/2;
        vector<vector<int>>dp(nums.size(),vector<int>(left+1,0));
        //初始化第一行dp数组
        if(nums[0] <= left) dp[0][nums[0]] = 1;
        dp[0][0] = 1;

        for(int i=1;i<nums.size();i++){
            for(int j=0;j<left+1;j++){
                if(j>=nums[i]) dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]];
                else dp[i][j] = dp[i-1][j];
            }
        }

        return dp[nums.size()-1][left];
    }
};

无法通过所有测试样例

原因：第一行数组初始化错误，nums[0]为0时，dp[0][0]为2

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int i=0;i<nums.size();i++) sum += nums[i];
        if (sum < abs(target) || (sum + target) % 2 != 0) return 0;//left一定要是偶数

        int left = (sum + target)/2;
        vector<vector<int>>dp(nums.size(),vector<int>(left+1,0));
        //初始化第一行dp数组
        if(nums[0] == 0) dp[0][0] =2;//不取加取
        else{
            if(nums[0] <= left) dp[0][nums[0]] = 1;
            dp[0][0] = 1;//不取nums[0]
        }

        for(int i=1;i<nums.size();i++){
            for(int j=0;j<left+1;j++){
                if(j>=nums[i]) dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]];//不取和取
                else dp[i][j] = dp[i-1][j];//不取
            }
        }

        return dp[nums.size()-1][left];
    }
};

为了避免分别讨论初始化第一行的不同情况，dp数组多加一行（类似于链表头节点）

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int i=0;i<nums.size();i++) sum += nums[i];
        if (sum < abs(target) || (sum + target) % 2 != 0) return 0;//left一定要是偶数

        int left = (sum + target)/2;
        vector<vector<int>>dp(nums.size()+1,vector<int>(left+1,0));
        //初始化第一行dp数组
        dp[0][0] = 1;

        for(int i=1;i<nums.size()+1;i++){
            for(int j=0;j<left+1;j++){
                if(j>=nums[i-1]) dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];//不取和取
                else dp[i][j] = dp[i-1][j];//不取
            }
        }

        return dp[nums.size()][left];
    }
};

优化：使用滚动数组（因为二维数组中只会用到左上角）

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

dp[j] += dp[j - nums[i]]

初始化的时候dp[0] 初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0

一维，从后往前遍历，完全背包为从前往后

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int i=0;i<nums.size();i++) sum += nums[i];
        if (sum < abs(target) || (sum + target) % 2 != 0) return 0;//left一定要是偶数

        int left = (sum + target)/2;
        vector<int>dp(left+1,0);
        dp[0] = 1;
        for(int i=0;i<nums.size();i++){
            for(int j=left;j>=0;j--){
                if(j>=nums[i])dp[j] = dp[j] + dp[j-nums[i]];
            }
        }
        return dp[left];
    }
};