题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
例子:背包重量为4
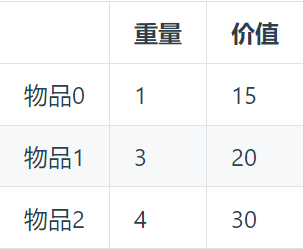
方法1:二维dp
1:确定dp数组,dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
2:确定递推公式,有两个方向推出来dp[i][j]:
不放物品i:由dp[i - 1][j]推出
放物品i:由dp[i - 1][j - weight[i]] + value[i]推出
3:初始化dp数组,
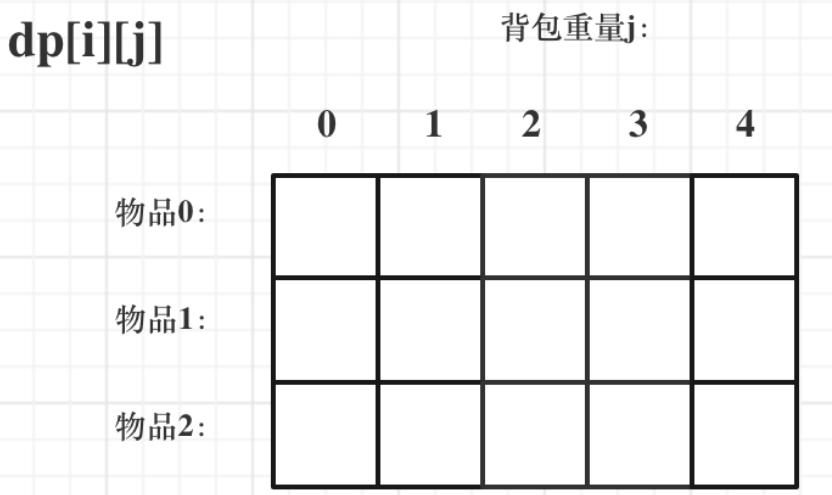
由递推公式可得,dp[i - 1][j]表示格子正上方,dp[i - 1][j - weight[i]]表示格子左上方,所以知道表格第一行与第一列,即可推出整个dp数组
第一列:背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0
第一行:j < weight[0]的时候,dp[0][j] 应该是 0,当j >= weight[0]时,dp[0][j] 应该是value[0]
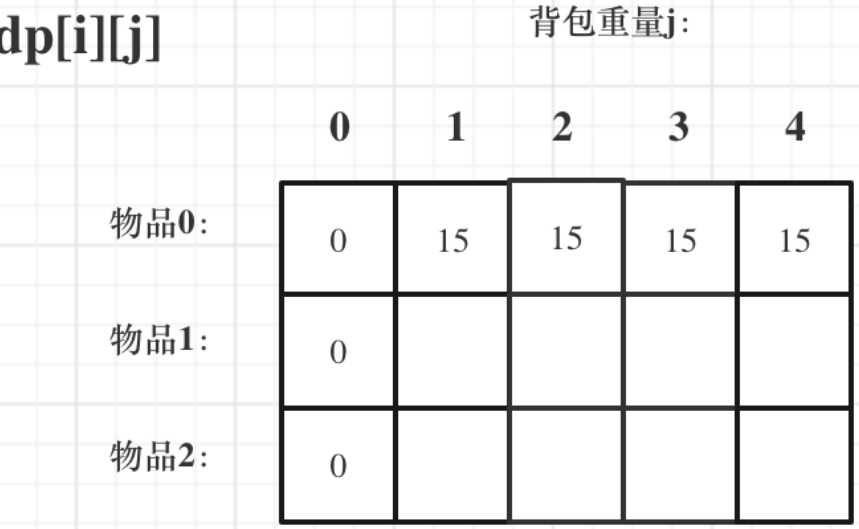
4:确定遍历顺序,先遍历物品和先遍历背包重量都可以推出完整dp数组
方法2:一维dp
思想:由于每次更新只会用到上一行数据,所以采用滚动数组的方法
采用倒序遍历,dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

